This is the first in a series of posts that help establish the mathematical framework of Proloquor.net’s core processes. Don’t worry, we won’t dive too deep, but we will need to start at the beginning to level-set. Here, we introduce the concept of probability, a core idea in all polling.
What Is Probability?
Probability is a measure of the likelihood of an event occurring in the future, based on information we have about the event. Many times, we can conclusively determine if an event will or will not happen. But most of the time, the conditions that determine an event are too complex to calculate, so the best we can do is assign a value describing its likelihood. Given an event E, we can define the probability that E will occur, P(E) with the following properties:
$$P(E) = \begin{cases}0 & \text{event E will definitely $not$ occur} \\ (0,1) & \text{event E $might$ occur} \\ 1 & \text{event E will $definitely$ occur} \end{cases}$$
So the value of probability is bounded between 0 and 1, proportional to the likelihood of the event.
Calculating Probabilities
So how do we use our knowledge of an event to calculate its probabilities? The simplest scenario is when we know practically nothing about the event and therefor must assume that all outcomes are equally likely. So if there are k possible outcomes and m of those outcomes correspond to event E, then:
$$P(E)= \frac{m}{k}$$
Consider rolling a single die and observing what number faces up. All we know is that there are 6 sides, numbered 1 through 6, and so each are equally likely. If we define event E as rolling a 4 (i.e. lands with ‘4’ facing up), then:
$$P(E)= \frac{1}{6}\approx0.167$$
since only 1 of the 6 outcomes that result in a 4. Alternately, we can multiply probabilities by 100 to express them as percentages; 16.7% in this case.
Now consider event A is that we roll an even number. Of the 6 possible outcomes, 3 of them (2, 4, and 6) result in that event, so:
$$P(A)= \frac{3}{6}=0.500$$
If we knew more about the weight distribution of the die, its aerodynamics, and the elasticity of the surface, we might be able to predict the outcome with more precision, but otherwise this is the best we do.
Combining Probabilities
There are a myriad of rules that help us calculate probabilities of complex events, but we’ll cover two of the basics here. Specifically let’s look at events that can be combined using the logical OR and AND operators.
Consider the following 2 events:
- A is rolling an even number on a single die
$$P(A)= \frac{3}{6}=0.500$$
- B is rolling an number less than 3 on a single die
$$P(B)= \frac{2}{6}\approx0.333$$
So what is the probability of the event of both A AND B occurring, or P(AB)? The formula for this is:
$$P(AB) = P(A) \times P(B|A)$$
P(B|A) is a conditional probability, or the probability of B, given that A has occurred. In other words, what is the probability that the roll is less than 3, given that the roll is even? Since there are only 3 outcomes that are even, but 1 of those is less than 3:
$$P(B|A) = \frac{1}{3} \approx 0.333$$
And so:
$$P(AB) = \frac{3}{6} \times \frac{1}{3} = \frac{1}{6} \approx 0.167$$
There’s a 16.7% chance that a roll will be both even and less than 3.
So now consider the probability of a roll being even or less than 3. The formula for that is:
$$P(A+B) = P(A) + P(B) – P(AB)$$
$$P(A+B) = \frac{3}{6} + \frac{2}{6} – \frac{1}{6} = \frac{4}{6} \approx 0.667$$
If you’re still struggling with these calculation, it often helps to lay out the outcomes and events in a Venn diagram:
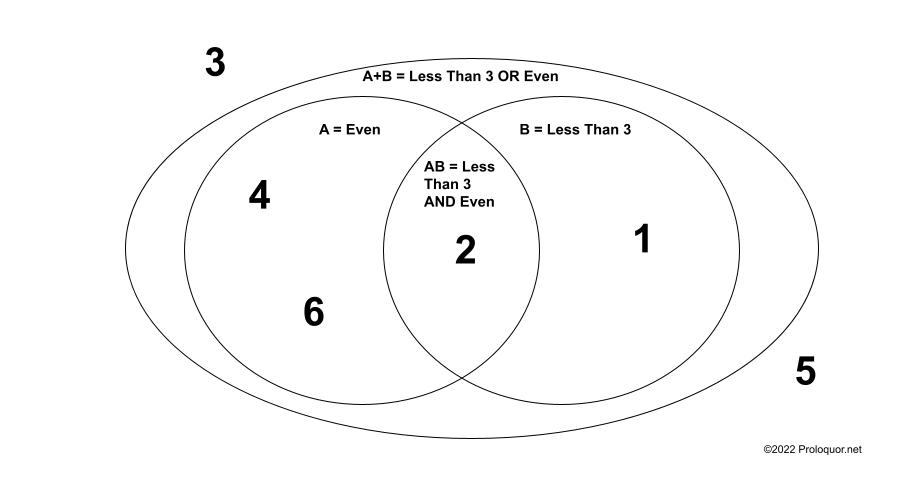
What’s Next?
We’ll re-visit probabilities often as we explore Proloquor.net’s processes. Probability distributions, hypothesis testing, regression and extrapolation are all tools that pollster’s use with a basis in probability.

